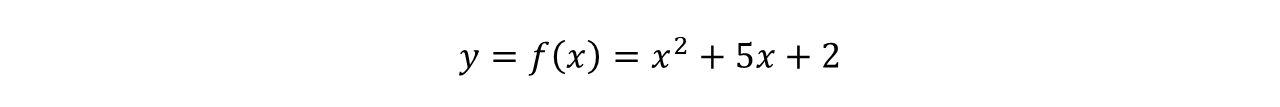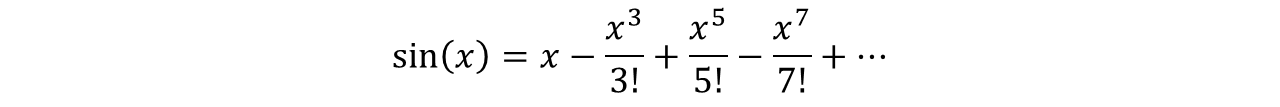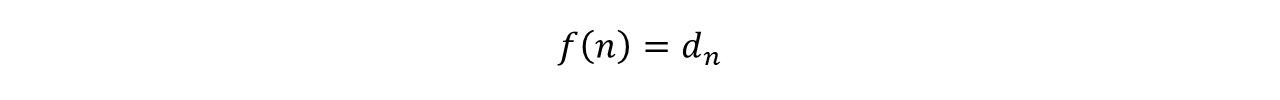Bubble, Bubble, AI's in Trouble
The obscenely high valuations of AI companies depend on a flawed philosophical argument for the inevitability of AGI
There has been much debate in the investment community about whether the large investments in Artificial Intelligence (AI) are justified or are rather evidence for a bubble. Last week, Goldman Sachs put out a “Top of Mind” report on whether AI is a bubble. Although the report featured one Artificial General Intelligence (AGI) gadfly, Gary Marcus, who said the Large Language Models (LLM) will not lead to AGI, the view that machines can have minds indentical to human minds, the general tenor was that current investment levels and valuations are reasonable. As Joseph Briggs, head of Goldman’s global economics team put it:
“Ultimately, we think that the enormous economic value that generative AI promises justifies the current investment in AI infrastructure, and that overall levels of AI investment appear sustainable as long as companies expect that investment today will generate outsized returns over the long run.”
Indeed, a series of recent large private transactions, in which insiders sold shares of OpenAI, valued the company at approximately $500 billion dollars. OpenAI is making plans to go public in 2026 or 2027, targeting a $1 trillion valuation and an additional capital raise of at least $60 billion dollars. And yet annualized revenues are expected to rise to about $20 billion dollars, implying a startling 50x multiple of revenues at a $1 trillion valuation. Although OpenAI consistently loses large amounts of money, these valuations would make it more valuable than SpaceX and perhaps the most valuable large startup in history.
However, reading through the Goldman report, we don’t get the business case that would justify enormous investments in AI. Will it come from AI agents? The report doesn’t make any argument that AI agents will fuel revenue increases that would justify the investments. As I have chronicled in a few posts, the current LLM models can’t function effectively as expert agents and no less a technical authority than Andrej Karpathy recently called AI agents “slop.”
Instead of rigorous realistic analysis of the coming AI applications, we get unbridled hope and optimism. For example, the report quotes David Cahn, a partner at Sequoia Capital as saying
“My closing thought would be, AI is going to change the world. People who try to narrow this down into AI-good or AI-bad are incorrect. AI is probably the most important technology of the next 50 years.
Similarly, the report quotes Byron Deeter, a partner at Bessemer Venture Partners:
“The AI investment opportunity is unprecedented. … So, AI truly represents the technology opportunity of our lifetimes. These developments will be discussed for generations, and our grandchildren will recount the early days of AI as a pivotal moment in history.”
If you look at other justifications for these eye-popping valuations of AI companies and the enormous level of investment, you see similar eruptions of praise and awe for a civilization-changing technology, but little discussion of just what the new technology will do that people will pay for.
Unbridled confidence along with no current business case is a classic warning sign of a bubble. We must suspect a bubble when we see very large investments being made based on hopes and dreams that are unlikely to be realized, with no current business case to back it up.
Where does this AI optimism come from? It is often claimed that the humanities have no practical applications, but hundreds of billions in AI investments as well as regulatory initiatives depend on the philosophical argument that the mind is an algorithm. Since the mind is a computer program, the impressive achievements of LLMs will soon lead to Artificial General Intelligence—AGI--and a looming economic cornucopia. Owning a share of the abundance machine, the thinking goes, must be immensely valuable.
The Unspoken Investment Thesis: AGI
The investment thesis that’s lurking behind these valuations is that AGI is coming soon, and that one or more of the frontier AI model development companies, such as OpenAI or Anthropic, will develop it. From the frontier companies, the AGI investment thesis is overt: Sam Altman, CEO of OpenAI, has been predicting that AGI is around the corner for a couple of years now, although he has recently backtracked a bit. Anthropic not only predicts the coming of AGI, but also warns about the dangers of an all-powerful AGI killing the human race. Shouldn’t you own a piece of such a omnipotent technology, preferably a large share? Many investors have answered yes.
Market analysts typically dance around the AGI question. Sometimes they talk about it explicitly. Other times, they make optimistic predictions that are tantamount to predicting imminent AGI. How could AI displace a large percentage of human jobs or discover new physical theories if it has not become AGI?
Ultimately, whether these large valuations are justified depends on whether we think AGI is possible, and if it is, whether it is also imminent. Belief in the possibility and indeed inevitability of AGI is very common, but it’s not clear where it comes from. The belief in AGI is not based on discoveries in neuroscience, cognitive science, or psychology. It seems to be founded on nothing more than sophisticated marketing.
The first highly sophisticated AI cheerleading happened decades ago with the publication of the extremely influential and popular book, Godel, Escher, Bach: An Eternal Golden Braid, by Douglas Hofstader. This book won a Pulitzer Prize and the National Book Award in 1980 and became the bible that animated the 1980s euphoria that AGI would be developed very soon. Of course, soon after an AI winter followed during which research enthusiasm and research grants withered, since none of the bold promises were realized.
Hofstader presented the standard philosophical view of AGI. The brain is the hardware, a biological computer, while the mind is the software that runs on the computer. If we can discover how to replicate the software that produces the mind, that is achieve AGI, we can run the software on any computer, including the standard silicon-based machines.
Rather than directly argue that the mind is a computer program, Hofstader goes through a series of analogies, stories, puzzles, and dialogues centered around the logician Godel, the illustrator Escher, and the composer Bach to suggest how mental states could arise from software. Essentially, the book says: “If the mind is software, here’s how our experience of consciousness and reason could emerge.” Hofstader presents an entertaining plausibility argument, but no direct demonstration that the mind really is nothing more than software. The reader must take on faith that the mind is an algorithm that could just as well run on a computer as on the brain.
David Chalmers To the Rescue
The AI fervor Hofstader inspired in the 1980s ended ignominiously in the 1990s. For many computer scientists, investors, and entrepreneurs, belief in AGI reverted to nothing more than an article of faith. In the mid-1990s, however, the philosopher David Chalmers came to the rescue with philosophical arguments that the mind is equivalent to software.
The medieval philosopher and theologian Thomas Aquinas imposed a philosophical architecture on Christian faith. For example, he famously provided five arguments for the existence of God in the Summa Theologica. It’s hard to overestimate Aquinas’s influence in Christian philosophy and natural theology: in 1567, he was declared the Angelic Doctor of the Catholic Church.
Chalmers is the AGI-faithful’s modern Thomas Aquinas. In his book The Conscious Mind: In Search of a Fundamental Theory, Chalmers has made a rigorous, very readable, and highly influential argument that the mind is an algorithm. In The Singularity: A Philosphical Analysis, Chalmers analyzed the commonly discussed singularity scenario, in which AGI is achieved and then improves itself to become superhuman. Singularity scenarios are behind the fear that AGI will kill all humanity, as the book If Anyone Builds it, Everyone Dies claims. Proponents of substantial AI regulation rely on this singularity argument.
It’s hard to overestimate Chalmers’ influence on the general public’s views of AI. Chalmers is articulate and personable and has spread his views beyond academia in debates and interviews, such as in the clip below. But few people have looked carefully at the substance of his arguments.
Chalmers’ Arguments
The Principle of Organizational Invariance
Chalmers’ bedrock claim is that consciousness arises from the functional organization of the brain. By functional organization, Chalmers means that the mind has an interlocking functional structure of parts that are all tied together. Each functional piece takes a set of inputs and produces an output. That output is one of the inputs to a different functional piece that also produces an output. Chalmers wants us to think of the functional structure as an abstraction, devoid of how it is actually implemented in the brain. In principle, you could draw a (very, very) large diagram of the functional organization of the brain. All that would be necessary is to list the inputs for each functional unit, the rules for determining the outputs, and how the functional units are tied together.
What the inputs and outputs actually are is irrelevant. They could be electrical signals in a neuron. They could also be electrical signals in a semiconductor. They could even be changes in water pressure. Chalmers’ principle of organizational invariance says that systems with the same functional organization will have the same conscious states, regardless of how the inputs and outputs are implemented physically. Thus, if a brain, a computer, and a series of water pipes have exactly the same functional organization, they will have the same conscious experience.
Chalmers justifies the principle of observational invariance by performing a thought experiment. Starting with a brain, he imagines removing just one functional piece from it and replacing it with an artificial unit that has exactly the same functionality. For example, you could imagine removing just one neuron and replacing it with an artificial semiconductor neuron that has exactly the same electrical inputs and outputs. Once you’ve made the switch, the brain will function exactly the same as before, with identical thoughts and experiences. Now keep removing functional pieces of the brain and replacing them with functionally equivalent artificial pieces. In the limit, you would have a completely artificial brain, but it would be identical to the initial biological brain. The experimental subject would not have noticed the change at any step, but would now be an AI, with the same memories, thoughts, and feelings.
Fading and Dancing Qualia
The obvious objection to Chalmers’ argument is that the experimental subject would have noticed before he became an AI. His consciousness would have gradually faded out as more and more of his brain was replaced with artificial functionality.
Chalmers, like other philosophers, refers to subjective experiences as “qualia.” An example of a qualia is the subjective way we experience the color red in contrast to its objective characterization as a frequency of light. Another example of a qualia is the way we hear music as opposed to its objective existence as vibrating air. Fading qualia means that our experience of colors, sound, tastes, and our internal awareness of ourselves, our memories, and our thoughts, would gradually diminish and then vanish. The objection to Chalmers’ argument then is that the subject would have noticed the fading qualia.
Chalmer doesn’t dismiss the logical possibility of fading qualia, but he finds fading qualia to be empirically implausible. A rational subject would have to be systematically wrong about everything if qualia really could fade. For example, if the qualia of red has faded to be a pale pink, and the qualia of despair is muted so that the subject barely feels any emotion, how can a rational being gush about the vivid red flowers he sees or complain about the angst he feels? A rational subject can’t talk about his inner life without his internal experiences being true.
Chalmers’ makes what he thinks of as a more powerful rebuttal in his “dancing qualia” argument. Chalmers imagines that we experiment with the subject, removing functional pieces of the brain until we discover the combination that causes them to flip qualia. For example, suppose there is some combination of functional pieces that when replaced flips the internal experience of red to blue. Now insert the artificial functional pieces but keep the biological pieces as well. Then install a switch that allows the experimenter to flip between using biological functionality and artificial functionality.
Suppose the subject is talking about a rose he sees in front of him. While he is talking, the experimenter would flip the switch back and forth so that internally the subject perceives red as he always did but also perceives that the rose is colored as what he would have formerly described as blue. Chalmers finds it highly implausible that qualia could dance back and forth with a flip of the switch without a rational subject noticing. How would the current experience of a blue rose, for example, be consistent with memories of a red rose?
Because Chalmers rejects fading and dancing qualia (and other variations such as suddenly disappearing qualia), he finds the principle of organizational invariance highly plausible, implying that it should be possible to build conscious machines once we understand the functional organization of the mind. Since software can simulate any functional organization, it must be possible to implement a conscious mind in software.
Are Chalmers’ Arguments Valid?
Chalmers argument rests on a critical assumption that he can’t prove to be true: that the mind can be described in terms of some functional organization. We don’t know that. The mind could be a product of some new physical process that we currently have no theory for. The mind might be a physical process but not covered by quantum mechanics or any other theory we currently have. We simply don’t know. Assuming the mind can be described as a functional organization is pure speculation.
Chalmers’ arguments also depend on a thought experiment. Although thought experiments can be useful in science, sooner or later you must perform the actual experiment to confirm your theory. Chalmers can only make plausibility arguments about the outcome of such an experiment, assuming it could be performed, but we don’t know what the real outcome would be until we try it.
But even if we grant Chalmers’ premise that the mind has a functional organization, his argument fails at the step in which it’s claimed that any function can be simulated or computed by a computer program. It’s a surprising mathematical fact that most functions can’t be simulated or computed by a computer program. Although there are an infinite number of computer programs, there is a much larger infinity of functions. There are infinitely more functions than there are computer programs and so almost all functions can’t be computed. In fact, knowing nothing about the functional organization of a mind, assuming there is one, if you chose possible functions at random to implement a mind, the probability is 100% you would choose non-computable functions, implying that AGI isn’t possible.
Why Aren’t All Functions Computable?
It might seem a strange question to ask whether all functions are computable. We are used to seeing functions written down in mathematical language, making them automatically computable. For example, the quadratic function is obviously computable:
We can put any x into this function and calculate the answer. For example, f(2) is 4 + 10 + 2, or 16. Or to take another example, the sine function is computable since we can write it as an infinite series:
We can put any x into this function and calculate sin(x) to any precision we like by including as many terms as we need in the infinite series. Surprisingly, however, there are an infinite number of functions that we can’t compute. The reason is that there are more functions than there are programs to compute them.
How Many Possible Computer Programs Are There?
A computer programs is a sequence of characters of a finite, but arbitrarily large length. For example, the python program below computes the function below it.
def quadratic_function(x):
return x**2 + 5*x + 2The program takes in x and then squares it, adds five times x to it, and then adds 2. It then returns the answer.
That program could be represented as the string of characters in which we include characters for a space, a carriage return, and a tab. All computer programs can be written as strings of characters of finite length. How many possible computer programs are there? It would seem that there are an infinite number of possible compute programs, but we’ll need to be more precise about what we mean by infinity.
Countable Infinity
A set is countably infinite if it can be put in order and counted by the infinite positive integers. This definition immediately leads to surprising consequences. The set of even numbers is countably infinite since the even numbers can be put in order and counted by the positive integers.
There are just as many even numbers as there are all numbers. Thus, it turns out that a subset of a countably infinite set is also countably infinite. When we are talking about infinite numbers, a subset of an infinite set has the same number of elements as the set itself.
What about the rational numbers? They are countably infinite as well, since we can put them in order and count them by the positive integers:
In this diagram, we order the rational numbers by following the arrows, excluding the rational numbers circled in green, since we already counted them previously. 1/1 would be the first element, counted as the first rational number, 1/2 would be second, counted as the second rational number, 2/1 would be the third element, counted as the third rational number, and so on.
Uncountable Infinity
What about the real numbers? The mathematician Georg Cantor discovered the surprising fact that there are infinitely more real numbers than there are rational numbers. Cantor proceeded by contradiction. Let’s assume we can order the real numbers by putting them into a one-to-one correspondence with the natural numbers as in the diagram below. Note that we have circled the diagonal element in each real number.
Cantor pointed out that we can construct a new real number with the property that its first digit is different from the first digit of the first real number, its second digit is different from the second digit of the second real number, and so on:
This new real number can’t be on the list, a contradiction, since we assumed that we counted all the real numbers. Our original supposition that the set of real numbers is countable must then be false. As a consequence, there are more real numbers than there are integers or rational numbers. Even if you think you’ve written down an infinite set of real numbers, there are always more. The set of real numbers isn’t countable: it’s uncountably infinite.
Is The Set of Possible Computer Programs Countably or Uncountably Infinite?
The set of all possible computer programs is countably infinite since we can order them. Every computer program is a sequence of character symbols of finite length. To order them, we can consider all legitimate computer programs that have one character, all legitimate computer programs that are two characters in length, etc. We can order them by placing the one-character programs first (counting only those that are legitimate, if any, in the programming language we are using), then the two- character programs next, and so on. Within the programs of character length N, we can also order them further by defining rules that order sequences of characters: if the first letter is “a”, it comes before any program that begins with any other letter or symbol, including “A” with the rule that lower case letters are counted before upper case letters. If both programs begin with “a,” then we proceed to the next character and apply the same ordering rules. In this way, we can associate every legitimate program with a positive integer. The set of all possible legitimate programs is countably infinite. There are as many possible computer programs as there are integers or rational numbers.
How Many Functions Are There?
The number of functions is uncountably infinite. To see this, let’s define a family of functions as follows: for every real number, the function is
where n is a positive integer and dn is the nth digit in the infinite decimal expansion of some real number. We can define one such function for every real number, implying that this subset of all the functions is uncountably infinite. Since there are more functions than there are algorithms to compute them, there must be an infinite number of functions that are not computable.
Chaitin’s constant is an example of a real number that can’t be computed by a computer program. Chaitin’s constant is the probability that a randomly generated computer program will halt. These probabilities are non-computable. They can be approximated, but not to arbitrary precision.
The Probability of AGI is Zero Under Chalmers’ Hypothesis
Chalmers assumes that the mind has a functional organization but makes no claim about what those functions happen to be. Let’s assume then that Nature (or God) chose the functions at random from the set of all possible functions, a reasonable view given that we have no idea what the functions might be. The set of functions Nature chooses from are the countably infinite functions that can be computed by a computer program and the infinitely larger uncountable set of functions that can’t be computed.
If you choose from a set at random that contains a countable and uncountably infinite set of elements, it’s a mathematical fact that the probability is 100% that you would choose one of the uncountably infinite elements, since there are infinitely more of them. Thus, even if the mind did have a functional organization, the probability is 100% that the functional pieces can’t be computed by any computer program. AGI then is not possible.
Conclusions
Elon Musk is fond of saying that experience unfolds in such a way as to maximize irony. That gigantic investments in AI could hinge upon a widely believed philosophical argument that AGI is possible, even though very few people understand the details of that argument, is peak irony.
When we examine the details of the argument for the possibility of AGI, it falls apart under scrutiny. If we have no reason to believe that AGI is just around the corner, and if startling high investment and valuations depend on the appearance of AGI in the next few years, we are in the midst of a classic investment bubble. At some unfortunately unpredictable point, we should expect those unsupportable valuations and the generally high asset prices that depend on them, to come crashing down.
An AI bubble doesn’t mean that AI will not turn out to be immensely useful and important, however. It just means that investment capital is currently misaligned with reality. The crash of AGI mania will free up capital to be deployed into more defensible and productive AI technologies. The sooner that happens, the better.